Közelítő módszerek hosszútávú átmeneti valószínűség számítására
Advisor
Sykora Henrik
Email
sykora@mm.bme.hu
Type
BSc MSc TDK
Language
hungarian english
Introduction:
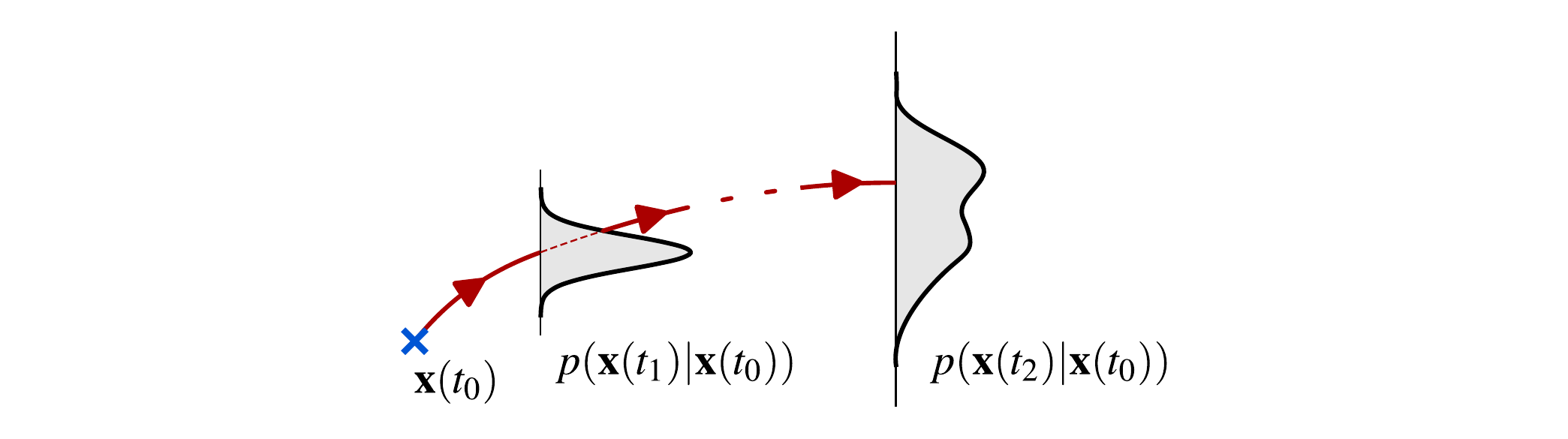
Egy sztochasztikus dinamikai rendszer leírásának egy fontos eszköze az átmeneti valószínűség: a rendszer egy adott állapotából mekkora valószínűséggel kerül át egy másikba. Egy új modelleilesztési eljárás ennek a mennyiségnek a hatékony számítására alapul: a módszer egy adott rendszeren mért jel megvalósulásának valószínűségét közelíti egy adott modell esetére, és az illesztett sztochasztikus dinamikai modell paramétereit aztán úgy hangolja, hogy ez a valószínűség maximális legyen. Az, hogy milyen módszerrel közelítjük ezt a valószínséget, alapjaiban határozza megy a modell paramétereinek becslésének minőségét, pontosságát. Abban az esetben, ha a dinamikai rendszereken végzett mérések mintavételezés elegendően nagy frekvenciájú a rendszer dinamikájához képest (pl. egy alacsony sajátfrekvenciájú rezgőrendszeren elvégzett mérés), az egyszerű közelítési módszerek is jól alkalmazhatóak. Viszont, ha a rendszer dinamikájához képest csak hosszú időközönként áll rendelkezésre mérés (pl.: magas frekvenciás rezgések mérése, repedés terjedése) .A dolgozat célja az átmeneti valószínűség meglévő közelítő módszereinek vizsgálata, újak kidolgozása és alkalmazása.Tasks:
- Irodalomkutatás dinamikai rendszerek átmeneti-valószínűség számítási módszereiről- Átmeneti-valószínűségszámítási algoritmusok implementálása
- Átmentei valószínűségszámítási algoritmusok összehasonlítása pontosság és számítási igény szempontjából
- (+1) Átmeneti-valószínűség alapú modellillszetés szintetikus adatsorokra
! A téma feldolgozásához szükséges módszerek túlmutatnak a képzés törzsanyagán így BSc szakdolgozat készítésének előfeltétele a témában készített TDK dolgozat !
A projekt kidolgozása során az alábbi, kerettantervben nem szereplő, vagy csak röviden érintett jártasságok szerezhetőek, elmélyíthetőek:
- Időfüggő véletlenszerű hatások modellezése és szimulációja dinamikai rendszerek esetén
- Véletlen hatásokkal gerjesztett (sztochasztikus) dinamikai rendszerek analízise, vizsgálata
- Korszerű statisztikai módszerek alkalmazása dinamikai rendszerek adatvezérelt (data-driven) illesztésén és analízisén keresztül
- Nagy teljesítményigényű számítások programozása