Nem minimális számú koordináták használata robotok dinamikai feladatainak megoldásában
Témavezető
Bodor Bálint
Email
bodor@mm.bme.hu
Típus
BSc MSc TDK
Nyelv
magyar angol
Bevezető:
A többtest-dinamikai rendszerek mozgásának leírására sokszor minimális, tehát a szabadsági fokok számával megegyező, független koordinátát használunk (ennek módját a Rezgéstan c. tantárgy keretében meg is tanultuk). Azonban vannak olyan esetek, például a zárt kinematikai láncú robotok esete is, amikor célravezetőbb lehet a nem minimális számú koordináták használata.Erre jó példa a képen lévő 2 DoF robot is, ahol két kar szöghelyzetét választva koordinátáknak, azok nem fogják a robot konfigurációját egyértelműen megadni. Azonban a C, D, E csuklók x,y koordinátáival a robot konfigurációja egyértelműen megadható. Célszerű lenne tehát a dinamikai egyenleteket is ezeknek a felhasználásával felírni.
Ilyenkor azonban a mozgásegyenletben szereplő koordináták nem függetlenek, közöttük geometriai kényszerek állnak fent. A rendszer mozgását így nem közönséges differenciálegyenletekkel (ODE) írjuk le, hanem differenciál algebrai egyenletekkel (DAE), amelyek tehát a koordinátákra vonatkozóan differenciálegyenletek, és algebrai egyenletek összességét jelentik. Ezen koordináta választás előnyei ellenére néhány kihívás is rejlik a rendszer mozgásának szimulációjában.
A téma keretében az a célunk, hogy megismerjük a mozgások leírásának ezt a módját, illetve hogy ennek felhasználásával az inverz dinamikai feladat megoldását is tanulmányozzuk.
Feladatok:
-Robotok mozgásegyenletének felírása és numerikus megoldása (minimális és nem minimális számú koordináta használatával)-Az inverz dinamikai feladat megoldásának tanulmányozása
-Szimulációk készítése (pl. MATLAB környezetben)
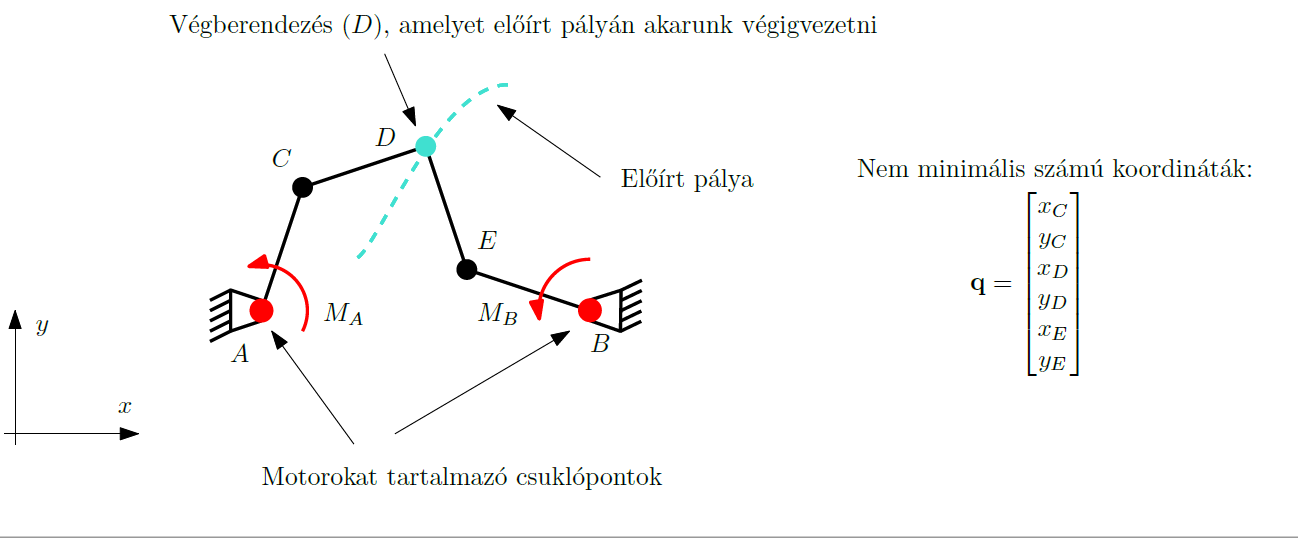
Zárt kinematikai láncú 2 DoF robot

